¡Tu carrito actualmente está vacío!
El análisis de algoritmos es fundamental en el desarrollo de software para optimizar el uso de recursos como el tiempo de ejecución y el consumo de memoria. El artículo de Amalia Duch (2007) aborda diversos aspectos del análisis de algoritmos, centrándose en los costes en tiempo y espacio, la notación asintótica y el análisis de algoritmos recursivos e iterativos. Aquí te proporciono un resumen, análisis y ejemplos clave de cada sección.
1. Complejidad en Tiempo
La complejidad en tiempo se refiere al tiempo que un algoritmo tarda en ejecutarse a medida que crece el tamaño de los datos de entrada. El objetivo de este análisis es entender cómo varía el tiempo de ejecución en función de la entrada del algoritmo.
Ejemplo: Búsqueda Lineal
Imagina que tienes una lista de números y deseas encontrar un número específico dentro de ella. La búsqueda lineal consiste en recorrer la lista uno por uno hasta encontrar el número deseado. En el peor de los casos, si el número que buscas está al final de la lista o no está en ella, tendrás que recorrer toda la lista.
Complejidad: O(n), ya que el tiempo de ejecución es proporcional al tamaño de la lista (n).
Ejemplo: Búsqueda Binaria
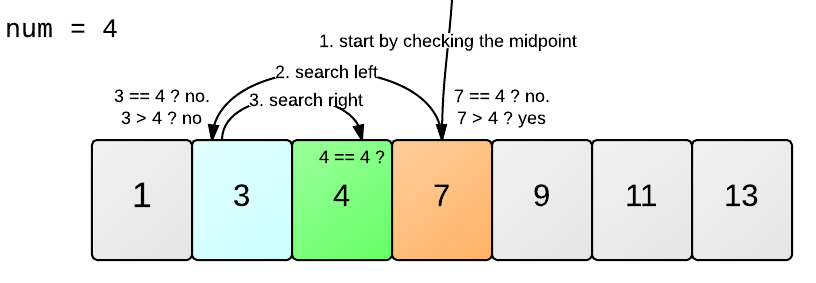
Por otro lado, si la lista está ordenada, se puede usar la búsqueda binaria, que consiste en dividir la lista a la mitad en cada paso, comparando el número con el valor central. Si el número es mayor o menor, se descarta la mitad de la lista.
Complejidad: O(log n), lo que significa que el tiempo de ejecución crece logarítmicamente conforme crece el tamaño de la lista, lo cual es mucho más eficiente que la búsqueda lineal.
Notación de Complejidad en Tiempo:
O(1): Tiempo constante. El tiempo no depende del tamaño de la entrada. Ejemplo: Acceder a un elemento específico de un arreglo por índice.
O(n): Tiempo lineal. El tiempo de ejecución crece proporcionalmente con el tamaño de la entrada. Ejemplo: Búsqueda lineal.
O(n²): Tiempo cuadrático. El tiempo crece con el cuadrado del tamaño de la entrada. Es típico en algoritmos con bucles anidados. Ejemplo: Algoritmo de ordenamiento por burbuja.
O(log n): Tiempo logarítmico. El tiempo de ejecución crece de manera logarítmica conforme aumenta el tamaño de la entrada. Ejemplo: Búsqueda binaria.
2. Complejidad en Espacio
La complejidad en espacio se refiere a la cantidad de memoria que un algoritmo necesita para ejecutarse. Esto también depende del tamaño de la entrada. Algunos algoritmos requieren más memoria que otros, lo cual es importante tener en cuenta, sobre todo cuando trabajamos con dispositivos con recursos limitados.
Ejemplo: Algoritmo de Ordenamiento por Burbuja
El ordenamiento por burbuja compara elementos consecutivos en una lista y los intercambia si están en el orden incorrecto. Este proceso se repite hasta que toda la lista está ordenada.
Complejidad en espacio: O(1), ya que el algoritmo solo necesita un espacio constante adicional para almacenar datos temporales durante las comparaciones e intercambios, sin importar el tamaño de la lista.
Ejemplo: Algoritmo de Ordenamiento por Fusión (Merge Sort)
El ordenamiento por fusión divide la lista en partes más pequeñas y las combina de manera ordenada. En este caso, el algoritmo necesita almacenar las sublistas mientras las procesa.
Complejidad en espacio: O(n), ya que requiere espacio adicional proporcional al tamaño de la lista.
Notación de Complejidad en Espacio:
O(1): Espacio constante. El algoritmo usa una cantidad fija de memoria, sin importar el tamaño de la entrada.
O(n): Espacio lineal. El algoritmo usa memoria proporcional al tamaño de la entrada.
3. Notación Asintótica
La notación asintótica se utiliza para describir el comportamiento de un algoritmo cuando el tamaño de la entrada tiende a infinito. Nos ayuda a medir la eficiencia de un algoritmo en situaciones extremas, ya que la complejidad real del algoritmo puede depender de factores como el tipo de datos, la implementación, o incluso la arquitectura del sistema.
Notación más común:
O (grande): Representa el peor de los casos, o el comportamiento más lento de un algoritmo. Ejemplo: En el peor de los casos, la búsqueda binaria tiene una complejidad de O(log n).
Ω (omega): Representa el mejor de los casos, o el comportamiento más rápido de un algoritmo. Ejemplo: En el mejor de los casos, un algoritmo de ordenamiento ya tiene los datos ordenados, lo que podría dar una complejidad de O(n).
Θ (theta): Representa la complejidad cuando el algoritmo tiene un comportamiento tanto en el caso peor como en el mejor. Se dice que un algoritmo tiene una complejidad Θ(f(n)) si su comportamiento es O(f(n)) en el peor caso y Ω(f(n)) en el mejor caso.
4. Resumen de Complejidades y Ejemplos
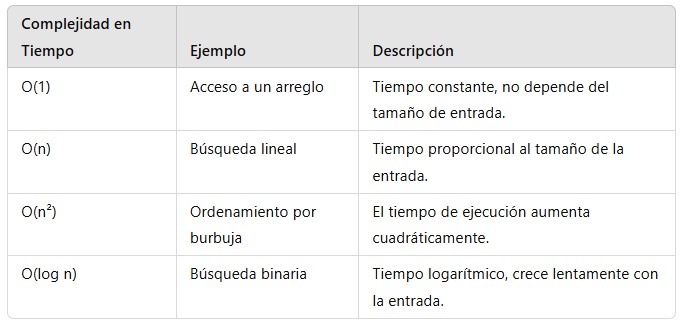
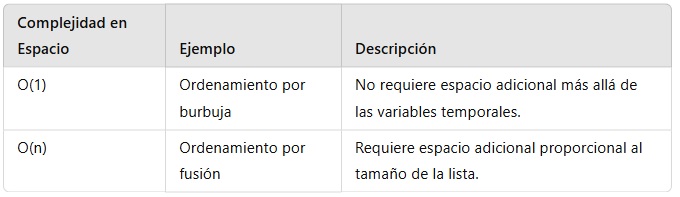
En Fin…
El análisis de complejidad en tiempo y espacio es esencial para entender el rendimiento de los algoritmos, especialmente en el contexto de aplicaciones que manejan grandes volúmenes de datos. A través de la notación asintótica, podemos comparar diferentes algoritmos y seleccionar el más adecuado para un problema determinado. Esto nos permite construir sistemas más eficientes y escalables, optimizando tanto los recursos computacionales como la memoria disponible.
Deja una respuesta